How are levels stored in Eggerland Mystery?
This blog post is also available as a YouTube video:
Eggerland Mystery, released for MSX computers in 1985 is a puzzle game, containing 100 rounds of normal puzzles, 5 extra rounds for which you need a special password, and 20 bonus stages (although, the first ten are repeated).
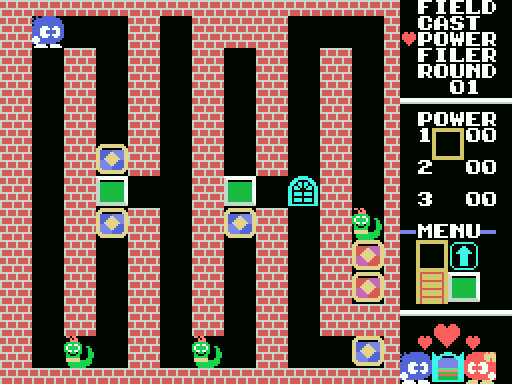
The first puzzle in the game, round 1, looks like this:
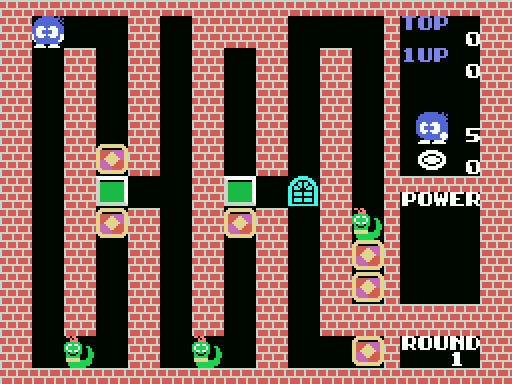
The goal is to pick up all the diamond framers, the yellowish blocks with the tilted square in the center. Once you pick all those up, the exit opens and you can progress to the next puzzle. There are of course enemies that will make your life difficult, but in round 1, it's just a couple of harmless Snakeys, that sit in your way.
To dig into the game, I will be using the built-in debugger in openMSX.
Table of contents:
- Determine where the current round number is stored
- Finding where the level data resides
- An initial look at the level data
- Finding the level data decoding algorithm
- Unraveling algorithm #1
- Unraveling algorithm #2
- Why two similar algorithms?
- Back to the first five bytes
- A mystery within Eggerland Mystery?
- What can we do with this information?
Determine where the current round number is stored
We need to start off somewhere, so let's find out where the game stores the current round number. That will be an interesting memory location to figure out, seeing as it will most likely be queried if we need to load the level data for a new round.
Let's use the Cheat Finder tool in openMSX, as this will allow us to pinpoint memory locations for changing values. We know that the round number will be 1 when we start the game, but that will be hard to locate, as surely there will be lots of values in memory containing 1. The game helps us though, because if we wait long enough in the intro screen, a demo of round 86 will play.
So, let's run the demo, and use the cheat finder to list all memory locations with value 86.
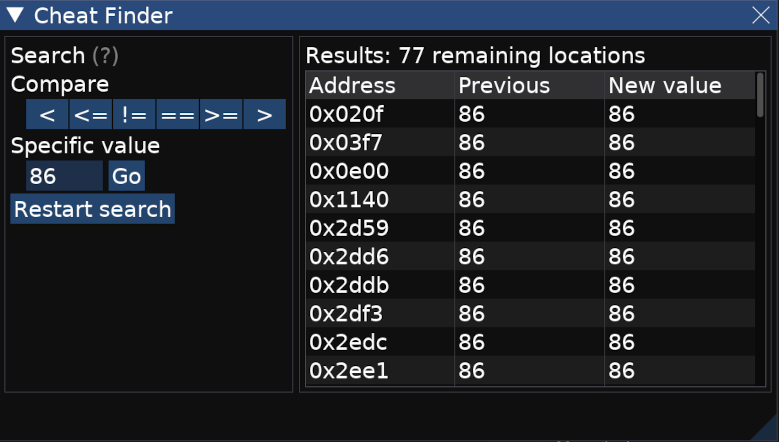
As you can see, it found 77 locations containing the value 86, so now we will simply start the actual game, and we will do another search, within these 77, for the value 1.
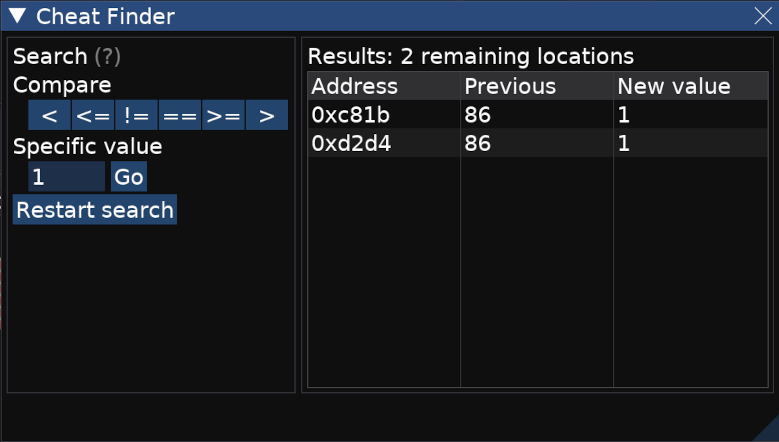
This has reduced the amount of results to only two memory locations! We're close. Let's finish the first level and do another check for the value 2.
Unfortunately, you'll notice that these two memory locations always keep in sync, and both contain the current
round number. In order to figure out which one contains the actual round number,
we can just force one of the values to a different number, exit the level successfully and see what happens. Let's
start with the first value in the list, at address 0xC81B.
In openMSX, we open the Debugger > Memory menu, navigate to address 0xC81B, and change it to let's
say 8.

If our assumption that this is the current round number is correct, then that will trick the game we are currently running round 8, and if we exit the level, we should end up in level 9!
Notice that the round number in the bottom right corner of the screen immediately changes when we changed the memory. This is obviously a very good sign.
In the video above, you can clearly see we are playing round 1, yet the round number in the bottom right corner shows 8, and when we exit the level it drops us in round 9.
The conclusion is that address 0xC81B does in fact contain the current round number.
Finding where the level data resides
Now that we have located the current round number, we put a watchpoint on this value, of type "read memory". That means that each time this value gets accessed in memory, the debugger will break, and we can check the disassembly window, and see the code that is being executed.
This is what we see when the first level is being loaded:
0x6716 3a 1b c8 ld a,($current_round)
0x6719 cd 24 a8 call #a824
0x671c 3a 1c c8 ld a,(#c81c)
0x671f a7 and a
0x6720 28 0a jr z,#672c
0x6722 3e 01 ld a,#01
0x6724 32 d0 d0 ld (#d0d0),a
The $current_round memory location, which is the name I gave to address 0xC81B is loaded
(with the ld instruction) into the a register,
which triggered our watch point.
Immediately after, there is a call instruction to address 0xA824, and another
ld instruction, which would overwrite the $current_round from
the first line. This indicates that we should probably take a deeper look into this function, as it will most likely
access the contents of the a register, so let's take a look at
what this function does.
0xa824 3a 1c c8 ld a,(#c81c)
0xa827 21 56 6d ld hl,#6d56
0xa82a a7 and a
0xa82b 28 06 jr z,#a833
0xa82d 21 80 6d ld hl,#6d80
0xa830 3d dec a
0xa831 18 04 jr #a837
0xa833 3a 1b c8 ld a,($current_round)
0xa836 3d dec a
0xa837 fe 05 cp #05
0xa839 38 06 jr c,#a841
0xa83b d6 05 sub #05
0xa83d 23 inc hl
0xa83e 23 inc hl
0xa83f 18 f6 jr #a837
0xa841 f5 push af
0xa842 7e ld a,(hl)
Apparently, our assumption is incorrect, as it does not seem to care about the current contents of the
a register! It immediately loads another value in a, namely
the contents of address 0xC81C. This is highly suspicious, as our current round number is in address is
in 0xC81B, and now we are loading the next byte after that.
Surely, these must be related.
For now, let's continue reading the first couple instructions of this function, and figure out what it does.
On line 0xA824 we load the value of our mystery neighbouring value in the a register.
On line 0xA827 we load the pointer 0x6D56 into the hl register.
The hl register usually contains a 16-bit pointer, so this is promising as well, this might point to a
memory location containing level data perhaps.
On line 0xA82A we AND the a register with itself. This seems useless at
first, but this instruction has a side-effect: it will set the zero flag if the
outcome of the AND operation is zero.
If the value we are AND-ing is for example 5, then we perform 5 AND 5, which is of course
5. Seeing as the result is not zero, the zero flag will not be set.
If we however AND 0 with 0, then the result will be 0 as well, so the zero flag will be set.
What we are actually testing for is whether the mystery neighbouring value is zero or not.
This is immediately obvious in the next instruction:
0xa82b 28 06 jr z,#a833
We do a relative jump if the z (zero) flag is set, to address 0xA833.
All you have to do is follow these jumps, and look at what code gets skipped. We see for instance that on line
0xA82D a different value gets loaded into the
hl register.
The equivalent pseudo code for these tests and jumps would be:
uint8_t data_at_6d56;
uint8_t data_at_6d80;
uint8_t round_number = ($mystery_neighbouring_value);
uint8_t* interesting_data = &data_at_6d56;
if ( round_number == 0 )
{
round_number = ($current_round);
round_number--;
}
else
{
interesting_data = &data_at_6d80;
round_number--;
}
Basically, we're pointing to a different set of data, depending on this mystery value being zero or not.
We also decrement the a register, containing either our mystery value, or the current round number.
This can be explained by the fact that the round number is 1-based. As soon as
we have to index into an array with level data, we can assume we want to address this with a zero-based index.
In our current state, the mystery value is in fact zero, so we take the path where the pointer is pointing to
0x6D56. Let's take a look in the memory viewer what can be found at that location.

Notice that address 0x6D56 and 0x6D80 are not far apart, in fact they're both in the
screenshot above. Unfortunately, that implies that this is not immediately the
level data we are looking for. Surely, these couple of bytes can't contain the level data for 125 rounds!
We'll have to look at some more of the code to figure out what is going on. Here's the section where we ended up,
after the if-clause from above:
0xa837 fe 05 cp #05
0xa839 38 06 jr c,#a841
0xa83b d6 05 sub #05
0xa83d 23 inc hl
0xa83e 23 inc hl
0xa83f 18 f6 jr #a837
0xa841 f5 push af
0xa842 7e ld a,(hl)
Our current state is: register a contains the round number - 1, and register hl points to
the data in the screenshot above.
The first thing we do now, is compare the a register, containing the current round number - 1 to the
hard-coded value of 5. For the first level, the a register would
contain zero, so if we compare zero to five, the side-effect of that comparison would be that the carry flag would
be set, because five is bigger than zero. The next jump instruction checks
the carry flag, and if it is set, we jump out of the little area we are investigating.
This doesn't give us much information, seeing as we are skipping the stuff we're interested in. So let's assume we
are currently looking at round 15, so the a register would
contain the value 14. The carry flag would not be set by the compare instruction and the jump would not be taken.
Next, we subtract the hard-coded value of 5 from the a register, which becomes 9, and we increment the
hl register twice. Then, we jump back to our original
comparison instruction and repeat the process, until the a register is smaller than or equal to five.
The equivalent pseudo code for this would be:
uint8_t* interesting_data = &data_at_6d56;
uint8_t current_round_minus_one = 14; // or whichever value, of course
while ( current_round_minus_one > 5 )
{
current_round_minus_one -= 5;
interesting_data++;
interesting_data++;
}
There's something off with our interesting_data variable, stored in the hl register
though. Why would we increment this value twice? Well, remember that the
hl register is used for 16-bit pointers, combined with the instruction we see after this little while
loop: at address 0xA842 we load the value of register
hl into the a register, meaning we do indeed treat what is in hl as a
pointer.
The conclusion we can draw here is that interesting_data does not point to level data itself, but to a
pointer! This makes that entire region of memory a list of pointers,
seemingly separated by 5 rounds each.
This actually makes sense, and the game gives us two hints that that might be the case:
- The construction mode in the game allows us to edit the first five levels.
- After every 5 levels in the game, you get to play a bonus stage.
It therefore makes perfect sense to separate level data per five rounds. Let's interpret that big list in memory as a list of pointers and see what we end up it. So this:

becomes this:
0xD5F80x6E590x6F970x70F20x720C0x734C0x74CC0x76090x77770x78CE0x7A240x7B940x7CEE0x7E460x7FC10x81120x82710x83EA0x85330x86530x87DB0x89550x8A7A0x89550x8A7A
Note that F8 D5 (the first pointer in the list) has been transformed into 0xD5F8. This is
because of
endianness, we have to swap the values around
if we want to interpret them as the full 16-bit values.
This list seems to contain 25 pointers, as I stopped when I encountered 00 00 00 00. Knowing that we
incremented the hl pointer for every 5 rounds, this makes perfect
sense. There are 100 regular rounds (so twenty pointers for those), 5 special rounds (one pointer for this) and 20
bonus rounds (four pointers for this), totalling 25 pointers!
There are a couple of interesting things going on with this list of pointers. Let's take a look at the four last
pointers. They seem to be two sets of the same two pointers. Another hint is
that the address to the first of these four is 0x6D80. Remember our
$mystery_neighbouring_value? The hard-coded pointers that were loaded were:
uint8_t data_at_6d56;
uint8_t data_at_6d80;
Address 0x6D56 was used in case that mystery value was zero, otherwise we would use
0x6D80, which points to these four last pointers.
Knowing that each pointer stands for 5 rounds, we have four pointers, so that makes 20 rounds, the first ten being
repeated twice (pointers 0x8955 and 0x8A7A), the
conclusion is pretty clear, these are the bonus stages that are defined in the four last pointers, and our mystery
neighbouring value is none other than the current bonus stage round number!
Let's call it $current_bonus_round.
Our complete function to locate the correct pointer to the level data now looks like this:
uint16_t normal_level_data_pointers[21];
uint16_t bonus_level_data_pointers[4];
uint8_t round_number = ($current_bonus_round);
uint16_t* level_data = &normal_level_data_pointers[0];
if ( round_number == 0 ) // this checks of course ($current_bonus_round)
{
round_number = ($current_round);
round_number--;
}
else
{
level_data = &bonus_level_data_pointers[0];
round_number--;
}
while ( round_number > 5 )
{
round_number -= 5;
level_data++;
}
// here we can use *level_data to access the five levels within this block
Another curious thing about this list of pointers is the address of the first one, compared to the 24 others. The 24
last ones all seem to be in the range 0x6E.. to
0x8A.., yet the first pointer is 0xD5F8. Let's take a look at how the memory is laid out
when the game is running.
We can determine that when the MSX loads the game, the ROM data is mapped at address 0x4000. Without
knowing how memory mapping works in the MSX, we can simply open up the
Eggerland ROM in a hex editor, and searching for F8 D5 59 6E..., basically the list of our 25 pointers.
This list is found at address 0x2D56 in the ROM, yet in game
the address is 0x6D56, a difference of 0x4000.
The ROM has a file size of 32 KB (0x8000), so that means our ROM is mapped from 0x4000 to
0xC000. The first pointer in our list of 25,
0xD5F8 is therefore pointing outside of the ROM data, somewhere in the RAM section.
To realise why this is the case, you do need to know how the game works, a bit. There is a built-in level editor in the game, the so-called construction mode. You can design 5 levels on your own, save them to disk and exchange them with friends. However, when you leave the construction mode, the 5 levels you designed will replace the actual first five levels of the game. This is done so you can actually play your custom designed levels. The construction mode can obviously not overwrite the data in ROM, so the first five levels need to be loaded in RAM, which can be perfectly overwritten, and then loaded and played by the game.
If we take a look at the second pointer in the list, as well as the first pointer, we see that the data for the first five levels is copied into RAM.
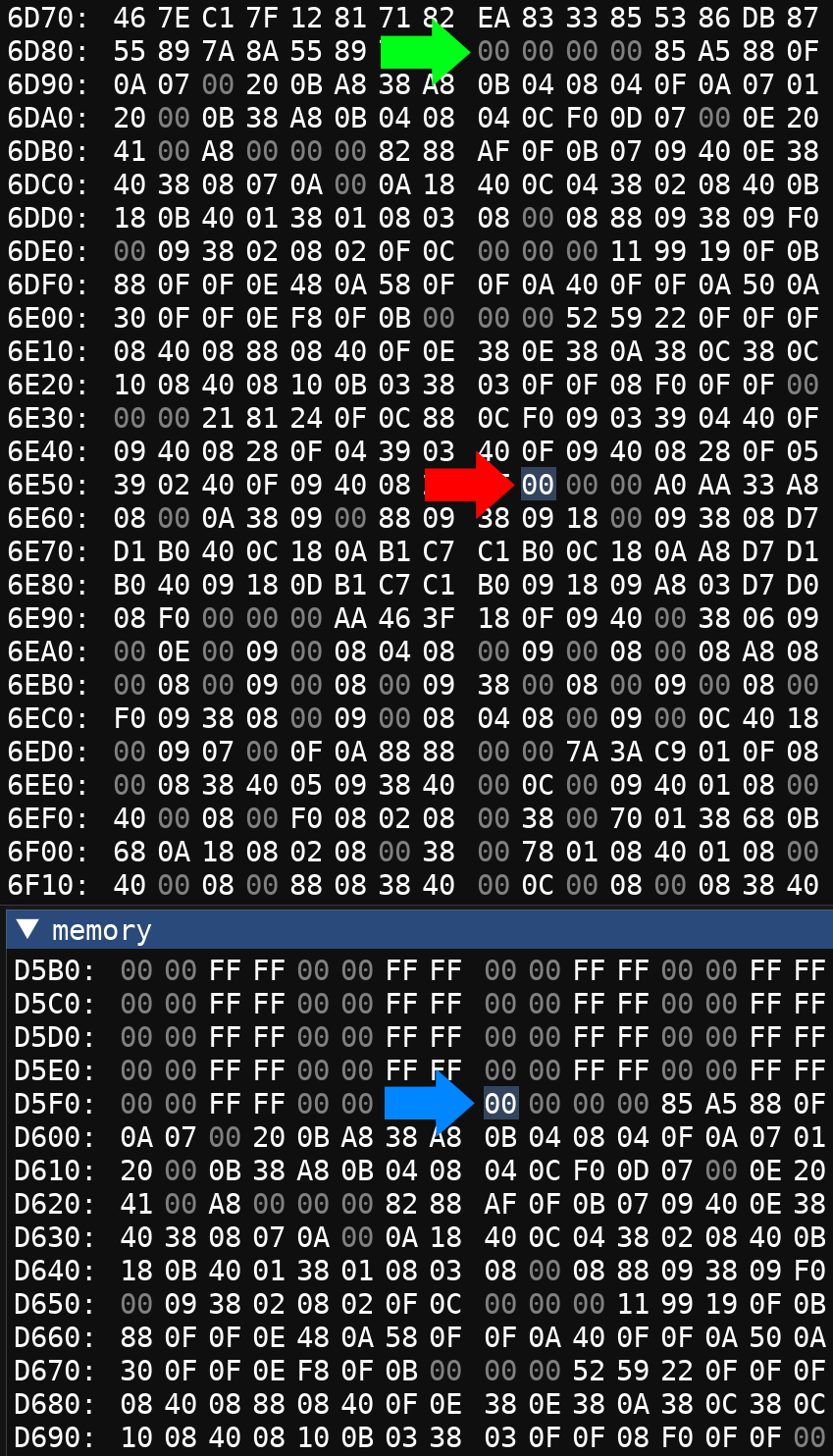
The blue arrow shows what the first pointer in our list points to, 0xD5F8, the first five rounds
located in RAM.
The red arrow shows what the second pointer in our list points to, 0x6E59, rounds 6-10, located in
ROM.
The green arrow however, does not appear in our list of 25 pointers, yet the data it represents is neatly positioned between our list of 25 pointers, and rounds 6-10. If we compare this data with what has been copied to RAM (the blue arrow), we determine it is identical, and is the location of the first five rounds in ROM. When the game starts up, it takes this data, and copies it over to RAM so it can be potentially overwritten by the construction mode.
Now that we have access to the level data, we can start interpreting how the data is encoded.
An initial look at the level data
Round 1 looks like this:

The data for the first five rounds, pointed to by our first pointer in the list 0xD5F8 looks like
this:
00 00 00 00 85 A5 88 0F
0A 07 00 20 0B A8 38 A8 0B 04 08 04 0F 0A 07 01
20 00 0B 38 A8 0B 04 08 04 0C F0 0D 07 00 0E 20
41 00 A8 00 00 00 82 88 AF 0F 0B 07 09 40 0E 38
40 38 08 07 0A 00 0A 18 40 0C 04 38 02 08 40 0B
18 0B 40 01 38 01 08 03 08 00 08 88 09 38 09 F0
00 09 38 02 08 02 0F 0C 00 00 00 11 99 19 0F 0B
88 0F 0F 0E 48 0A 58 0F 0F 0A 40 0F 0F 0A 50 0A
30 0F 0F 0E F8 0F 0B 00 00 00 52 59 22 0F 0F 0F
08 40 08 88 08 40 0F 0E 38 0E 38 0A 38 0C 38 0C
10 08 40 08 10 0B 03 38 03 0F 0F 08 F0 0F 0F 00
00 00 21 81 24 0F 0C 88 0C F0 09 03 39 04 40 0F
09 40 08 28 0F 04 39 03 40 0F 09 40 08 28 0F 05
39 02 40 0F 09 40 08 28 0F
If we look at this data for a bit, the triplet 00 00 00 seems to repeat suspiciously, like so:
00 00 00 00 85 A5 88 0F
0A 07 00 20 0B A8 38 A8 0B 04 08 04 0F 0A 07 01
20 00 0B 38 A8 0B 04 08 04 0C F0 0D 07 00 0E 20
41 00 A8 00 00 00 82 88 AF 0F 0B 07 09 40 0E 38
40 38 08 07 0A 00 0A 18 40 0C 04 38 02 08 40 0B
18 0B 40 01 38 01 08 03 08 00 08 88 09 38 09 F0
00 09 38 02 08 02 0F 0C 00 00 00 11 99 19 0F 0B
88 0F 0F 0E 48 0A 58 0F 0F 0A 40 0F 0F 0A 50 0A
30 0F 0F 0E F8 0F 0B 00 00 00 52 59 22 0F 0F 0F
08 40 08 88 08 40 0F 0E 38 0E 38 0A 38 0C 38 0C
10 08 40 08 10 0B 03 38 03 0F 0F 08 F0 0F 0F 00
00 00 21 81 24 0F 0C 88 0C F0 09 03 39 04 40 0F
09 40 08 28 0F 04 39 03 40 0F 09 40 08 28 0F 05
39 02 40 0F 09 40 08 28 0F
Could these be the individual levels?
00 00 00 00 85 A5 88 0F
0A 07 00 20 0B A8 38 A8 0B 04 08 04 0F 0A 07 01
20 00 0B 38 A8 0B 04 08 04 0C F0 0D 07 00 0E 20
41 00 A8 00 00 00 82 88 AF 0F 0B 07 09 40 0E 38
40 38 08 07 0A 00 0A 18 40 0C 04 38 02 08 40 0B
18 0B 40 01 38 01 08 03 08 00 08 88 09 38 09 F0
00 09 38 02 08 02 0F 0C 00 00 00 11 99 19 0F 0B
88 0F 0F 0E 48 0A 58 0F 0F 0A 40 0F 0F 0A 50 0A
30 0F 0F 0E F8 0F 0B 00 00 00 52 59 22 0F 0F 0F
08 40 08 88 08 40 0F 0E 38 0E 38 0A 38 0C 38 0C
10 08 40 08 10 0B 03 38 03 0F 0F 08 F0 0F 0F 00
00 00 21 81 24 0F 0C 88 0C F0 09 03 39 04 40 0F
09 40 08 28 0F 04 39 03 40 0F 09 40 08 28 0F 05
39 02 40 0F 09 40 08 28 0F
Luckily, the game gives us a huge hand by providing a construction mode where we can not only create our own levels, but it also loads the five first levels in the editor. That means we can actually alter the first level and see what changes we end up with in the exported file.
Let's open the construction mode, and export the first five levels to disk, and see what that file looks like in the hex editor.
The saved file looks like this:
FE F8 D5 C9 D6 00 00 00 00 00 00 85 A5 88 0F 0A
07 00 20 0B A8 38 A8 0B 04 08 04 0F 0A 07 01 20
00 0B 38 A8 0B 04 08 04 0C F0 0D 07 00 0E 20 41
00 A8 00 00 00 82 88 AF 0F 0B 07 09 40 0E 38 40
38 08 07 0A 00 0A 18 40 0C 04 38 02 08 40 0B 18
0B 40 01 38 01 08 03 08 00 08 88 09 38 09 F0 00
09 38 02 08 02 0F 0C 00 00 00 11 99 19 0F 0B 88
0F 0F 0E 48 0A 58 0F 0F 0A 40 0F 0F 0A 50 0A 30
0F 0F 0E F8 0F 0B 00 00 00 52 59 22 0F 0F 0F 08
40 08 88 08 40 0F 0E 38 0E 38 0A 38 0C 38 0C 10
08 40 08 10 0B 03 38 03 0F 0F 08 F0 0F 0F 00 00
00 21 81 24 0F 0C 88 0C F0 09 03 39 04 40 0F 09
40 08 28 0F 04 39 03 40 0F 09 40 08 28 0F 05 39
02 40 0F 09 40 08 28 0F
Other than the first 7 bytes, which seems to be some sort of file header, the level data is identical to what we found in RAM and ROM. Now, let's use the construction mode to clear out the first level, and assign some powerups.

For the level to be valid, Lolo and the exit have to be present. I have also added three diamond framers. The reason for this is because you can assign a number to each powerup, as visible in the screenhot: 01 for the arrow, 02 for the emerald framer and 03 for the bridge. This number indicates how many diamond framers you have to pick up before the powerup becomes available. This information has to be stored in the level data as well, so we might as well include it here.
The new save data looks like this, with the difference compared to the original data highlighted:
FE F8 D5 B7 D6 00 00 81 C2 43 46 56 13 0F 0F 0F
0F 0F 0F 0F 0F 0D 88 F0 0F 08 42 0F 0F 0F 0F 0C
00 00 00 82 88 AF 0F 0B 07 09 40 0E 38 40 38 08
07 0A 00 0A 18 40 0C 04 38 02 08 40 0B 18 0B 40
01 38 01 08 03 08 00 08 88 09 38 09 F0 00 09 38
02 08 02 0F 0C 00 00 00 11 99 19 0F 0B 88 0F 0F
0E 48 0A 58 0F 0F 0A 40 0F 0F 0A 50 0A 30 0F 0F
0E F8 0F 0B 00 00 00 52 59 22 0F 0F 0F 08 40 08
88 08 40 0F 0E 38 0E 38 0A 38 0C 38 0C 10 08 40
08 10 0B 03 38 03 0F 0F 08 F0 0F 0F 00 00 00 21
81 24 0F 0C 88 0C F0 09 03 39 04 40 0F 09 40 08
28 0F 04 39 03 40 0F 09 40 08 28 0F 05 39 02 40
0F 09 40 08 28 0F
A couple conclusions we can draw from this new data:
- The five rounds seem to indeed be separated by the three zeroes we suspected before. Round 2, left intact, does
seem to start with
00 00 00 82 88 AF ...which comes right after the highlighted section of the changed data above. - The first three zeroes of the new round 1 seem to have been replaced by
81 C2 43. What stands out here is that these three bytes end with 1, 2 and 3:81 C2 43. It seems quite coincidental to the amount of diamond framers you need to pick up to activate the powerups! It does make sense that the three first bytes are the powerup data, as for the first five rounds in the game, no powerups are available, hence the values being00. That's where our three00's come from! -
The data for round 1 now seems to be way shorter. This makes sense too, because the level is mostly empty. We see
a bunch of
0F's followed by some other numbers, and then a couple more0F's.
We've come as far as we can with the construction mode, now we'll have to look at the disassembly to figure out how this data is structured.
Finding the level data decoding algorithm
Finding the algorithm that decodes this level data shouldn't be that hard. We just have to put a "read memory" watchpoint on the first byte of the level data of round 1, and then start round 1 in the game. The level data should only be touched by the decoding function at that point in time.
Here's the code where we break when we put a watchpoint on address 0xD5F8, the first byte of round 1:
0xa4b0 11 7b d8 ld de,#d87b
0xa4b3 01 03 00 ld bc,#0003
0xa4b6 ed b0 ldir
0xa4b8 11 8a d8 ld de,#d88a
0xa4bb 01 02 00 ld bc,#0002
0xa4be ed b0 ldir
0xa4c0 11 00 c0 ld de,#c000
0xa4c3 c3 06 a5 jp #a506
We don't see any immediate reference to address 0xD5F8, but that makes sense. This routine has to be
able to decode all the rounds, not just the first. There must be a pointer
around that points to the current round. Let's look at what the ldir instruction does first.
The ldir instruction copies data from the memory location pointed to in the hl register to
the memory location pointed to in the de register. It does so
one byte at a time, but n amount of times, determined by the contents of the bc register. Every time it
is executed, it copies one byte, increments registers hl and
de, and decrements register bc until it reaches zero.
Looking at the code, the bc register is loaded with the hard-coded value of 3 in line
0xA4B3. This strengthens our suspicion that the first three bytes are related to
the powerups, as there are three possible powerups in each round.
The de register is loaded with the target pointer 0xD87B in line 0xA4B0. This
is an unknown memory location, but it does make sense that you would copy
the data out of the stored level data, and into some other location you can manipulate, for example when the powerup
has been used up. If you need to reference this data later on, you don't
want to have to look up what the current round is, find it in the 25 pointers, find the correct level data within
the block of 5 rounds, and look at those three bytes then. You'll want to put
this data in a fixed known location for easy access, which is exactly what the programmers of the game did.
The hl register is not explicitly set in this piece of code, it has been set before this function
was called, and it does indeed contain 0xD5F8 when we inspect it.
Basically, we are copying the first three bytes of our level data to some unknown location.
This is then immediately followed by a copy of the next two bytes to memory location 0xD88A. At this
time, we have no idea what these two bytes represent.
We now ended up here:
0xa4c0 11 00 c0 ld de,#c000
0xa4c3 c3 06 a5 jp #a506
We load address 0xC000 into the de register and jump away to address 0xA506.
Address 0xC000 is interesting, because if you remember the
memory layout, you will recall that the ROM was mapped at address 0x4000 and its size was
0x8000. Add the two together and you end up at address 0xC000.
We'll have to keep an eye on that memory location, it will most likely be involved in decoding the level data.
Now, we take a look at what code that unconditional jump we take leads us to:
0xa506 7e ld a,(hl)
0xa507 e6 7f and #7f
0xa509 47 ld b,a
0xa50a 7e ld a,(hl)
0xa50b 23 inc hl
0xa50c e6 80 and #80
0xa50e ca 5c a5 jp z,#a55c
0xa511 d5 push de
0xa512 3e 0b ld a,#0b
0xa514 32 12 d9 ld (#d912),a
0xa517 7e ld a,(hl)
0xa518 e6 07 and #07
0xa51a 4f ld c,a
0xa51b 0c inc c
0xa51c 7e ld a,(hl)
0xa51d e6 f8 and #f8
0xa51f 12 ld (de),a
0xa520 c5 push bc
0xa521 01 0b 00 ld bc,#000b
0xa524 eb ex de,hl
0xa525 09 add hl,bc
0xa526 eb ex de,hl
0xa527 c1 pop bc
0xa528 f5 push af
0xa529 3a 12 d9 ld a,(#d912)
0xa52c d6 01 sub #01
0xa52e 28 18 jr z,#a548
0xa530 32 12 d9 ld (#d912),a
0xa533 f1 pop af
0xa534 0d dec c
0xa535 20 e8 jr nz,#a51f
0xa537 23 inc hl
0xa538 10 dd djnz #a517
0xa53a 22 4d dd ld (#dd4d),hl
0xa53d d1 pop de
0xa53e eb ex de,hl
0xa53f 01 79 00 ld bc,#0079
0xa542 09 add hl,bc
0xa543 eb ex de,hl
0xa544 3e ff ld a,#ff
0xa546 12 ld (de),a
0xa547 c9 ret
Let's tackle this bit by bit. The hl register, at this point in time, contains a pointer to the sixth
byte of our level data (we copied the first three and subsequent two in the
previous section).
0xa506 7e ld a,(hl)
0xa507 e6 7f and #7f
0xa509 47 ld b,a
This code loads what hl is pointing to, the sixth byte, into the a register. For round 1,
this value is 0xA5.
Then, we AND this with the hard-coded value of 0x7F. It's easy to visualize both these
values in binary, to see what we're actually doing.
0xA5 = 1010 0101
0x7F = 0111 1111
----------------
AND = 0010 0101 = 0x25 (37 decimal)
Basically, when we AND with 0x7F, we ignore the top bit, and copy the bottom seven bits.
This leads us to the decimal value of 37, which we then load into the
b register.
We continue:
0xa50a 7e ld a,(hl)
0xa50b 23 inc hl
0xa50c e6 80 and #80
0xa50e ca 5c a5 jp z,#a55c
Because the previous AND operation messed with the value in the a register, we have to
reload that. Apparently, we're going to do something else with the sixth byte
of our level data.
The increase of the hl register isn't super relevant to our understanding of what happens
with the sixth byte, it just moves to hl pointer to the seventh
byte, for future processing. It does indicate however that what we are about to do next is all that will happen with
the sixth byte.
We again do an AND operation on our sixth byte, this time with the value 0x80. Let's look
at that in binary:
0xA5 = 1010 0101
0x80 = 1000 0000
----------------
AND = 1000 0000
This AND operation checks the top bit in the provided value. The reason why the exact outcome of this
operation isn't that relevant is because of the next jump instruction. This
jump is conditional on the zero flag. If the zero flag is set, the jump will be taken, if not we just carry on. This
means that the top bit in the sixth byte of the level data determines
whether we jump or not. Let's take a look at what we jump to, address 0xA55C, which is beyond the
current routine we are looking at:
0xa55c 7e ld a,(hl)
0xa55d e6 07 and #07
0xa55f 4f ld c,a
0xa560 0c inc c
0xa561 7e ld a,(hl)
0xa562 e6 f8 and #f8
0xa564 12 ld (de),a
0xa565 13 inc de
0xa566 0d dec c
0xa567 20 fb jr nz,#a564
0xa569 23 inc hl
0xa56a 10 f0 djnz #a55c
0xa56c 22 4d dd ld (#dd4d),hl
0xa56f 3e ff ld a,#ff
0xa571 12 ld (de),a
0xa572 c9 ret
Notice that both this new segment, and the remainder of our original code end with a return
instruction. The jump, conditional on the outcome of the top bit being set in the sixth
byte, chooses which section of code gets executed. That makes it a simple if clause:
if (top_bit_set_on_byte_six)
{
// execute lines 0xA511 to 0xA547
}
else
{
// execute lines 0xA55C to 0xA572
}
It looks like we have two algorithms to decode the level data, chosen by that top bit! Let's take a look at what we concluded from this disassembly so far:
- The first three bytes are related to the powerups, they get copied somewhere.
- The next two bytes are also copied somewhere else, but we don't know yet what they represent.
- The next byte is split into two values: the top bit determining which algorithm we use, and the bottom seven bits contain a yet unknown numeric value.
Before we dig into the disassembly to figure out what that numeric value means, let's take a look at our level data bytes for round 1 again:
00 00 00 00 85 A5 88 0F 0A 07 00 20 0B A8 38 A8
0B 04 08 04 0F 0A 07 01 20 00 0B 38 A8 0B 04 08
04 0C F0 0D 07 00 0E 20 41 00 A8
The total amount of bytes for round 1 is 43 bytes, as you can count above. The header (three bytes for powerups, two unknowns, and one byte we are currently thinking about) consists of 6 bytes. 43 minus 6 happens to be 37, which is the exact value we decoded by taking the bottom seven bits of our sixth byte! Clearly, it is the amount of bytes we need to process to decode the level. This also makes sense, as we already knew the level data for all the rounds had variable lengths. There is some sort of compression algorithm in play, and you need to know how many bytes to process to decode an entire level.
Also, seeing as the rounds are grouped per five for each of our 25 pointers, you need to be able to traverse this block of five, to get to for example the fourth level. You just need to read the sixth byte of each round, take the bottom seven bits, and skip that amount of bytes to reach the next round.
Unraveling algorithm #1
This is the first potential level-decoding algorithm we encountered, and this is chosen if the top bit of our sixth byte is actually set:
0xa511 d5 push de
0xa512 3e 0b ld a,#0b
0xa514 32 12 d9 ld (#d912),a
0xa517 7e ld a,(hl)
0xa518 e6 07 and #07
0xa51a 4f ld c,a
0xa51b 0c inc c
0xa51c 7e ld a,(hl)
0xa51d e6 f8 and #f8
0xa51f 12 ld (de),a
0xa520 c5 push bc
0xa521 01 0b 00 ld bc,#000b
0xa524 eb ex de,hl
0xa525 09 add hl,bc
0xa526 eb ex de,hl
0xa527 c1 pop bc
0xa528 f5 push af
0xa529 3a 12 d9 ld a,(#d912)
0xa52c d6 01 sub #01
0xa52e 28 18 jr z,#a548
0xa530 32 12 d9 ld (#d912),a
0xa533 f1 pop af
0xa534 0d dec c
0xa535 20 e8 jr nz,#a51f
0xa537 23 inc hl
0xa538 10 dd djnz #a517
0xa53a 22 4d dd ld (#dd4d),hl
0xa53d d1 pop de
0xa53e eb ex de,hl
0xa53f 01 79 00 ld bc,#0079
0xa542 09 add hl,bc
0xa543 eb ex de,hl
0xa544 3e ff ld a,#ff
0xa546 12 ld (de),a
0xa547 c9 ret
Our current state looks like this:
- Register
hlcontains a pointer to the seventh byte of our level data. - Register
decontains a pointer to0xC000, presumably a working area we will put the decoded level data into.
When you're confronted with a slightly longer function such as this one, it's always interesting to first take a
global look and look for things that stand out. There are a couple of
instructions that are necessary because of the limitations of the machine, such as all the stack pushing and
popping, and register exchanges (instructions push, pop,
ex), but they don't really affect our interpretation of what is going on.
The first thing I notice is this:
0xa512 3e 0b ld a,#0b
0xa514 32 12 d9 ld (#d912),a
We are loading the hard-coded value 0x0B into the a register, and saving it somewhere in
memory. 0x0B is of course 11 decimal. This stands out, because
an Eggerland round consists of a 11x11 board! To decode level data, surely we need to track our current x and y
positions, so loading 11 in memory is a good sign.
The next thing that stands out is this:
0xa517 7e ld a,(hl)
0xa518 e6 07 and #07
0xa51a 4f ld c,a
0xa51b 0c inc c
0xa51c 7e ld a,(hl)
0xa51d e6 f8 and #f8
0xa51f 12 ld (de),a
Register hl, containing our seventh byte of our level data, or rather the first byte of the actual
level, is being ANDed with 0x07 and 0xF8.
We've already seen a similar manipulation with the sixth byte, where we included the algorithm choice in the top
bit, and the data length in the bottom seven bits. Let's take a look at these
values in binary, to see how the split of these next bytes is done:
0x07 = 0000 0111
0xF8 = 1111 1000
Clearly, we are separating the bottom three bits from the top 5 bits. If we now look at the same piece of code, and see what we actually do with these extracted values, we see this:
0xa517 7e ld a,(hl)
0xa518 e6 07 and #07
0xa51a 4f ld c,a
0xa51b 0c inc c
0xa51c 7e ld a,(hl)
0xa51d e6 f8 and #f8
0xa51f 12 ld (de),a
The bottom three bits are stored locally in the c register, which is then incremented by 1. The top
five bits get copied over to 0xC000, the pointer that resides in
register de.
The next section does some shuffling around with pointers, but we do see #000b popping up again,
another representation of the decimal value 11!
0xa520 c5 push bc
0xa521 01 0b 00 ld bc,#000b
0xa524 eb ex de,hl
0xa525 09 add hl,bc
0xa526 eb ex de,hl
0xa527 c1 pop bc
At the beginning and end of this section, we are pushing and popping the stack. Our c register did
contain the bottom three bits, and we don't want to lose this information, yet
we do need to work with the c register for some reason. By pushing and popping, we ensure we can mess
with these register, without losing track of our original bottom three bits.
The add instruction does the bulk of the work here, it adds the value of the bc register,
which we load with the value 11, to the pointer that is in hl.
Before we do that though, we exchange registers de and hl, and swap them back after we do
our addition. Again, this convoluted process is just a result of the
limitations of the machine: the add hl,bc instruction exists, the add de,bc instruction,
which would have been perfect for this situation, simply does not, so we have
to swap some data around.
We are adding 11, not to our seventh byte which resided in hl, but to the 0xC000 pointer!
Next, we again do something that is level coordinate related:
0xa528 f5 push af
0xa529 3a 12 d9 ld a,(#d912)
0xa52c d6 01 sub #01
0xa52e 28 18 jr z,#a548
0xa530 32 12 d9 ld (#d912),a
0xa533 f1 pop af
At the start of the function, we had loaded the hard-coded value 11 into memory location 0xD912. Now,
we simply load that value back into the a register, subtract one
from it, check whether it is zero and jump somewhere outside of this function if it is, and save the decremented
value back to memory address 0xD912.
In short, we are keeping track of two 11-related counters. The first one, kept at address 0xD912, which
is decremented and checked for zero, and the second one, by jumping 11
places forward in our decoding destination memory starting at 0xC000. Makes perfect sense when we are
dealing with an 11 by 11 board.
Next up is this:
0xa534 0d dec c
0xa535 20 e8 jr nz,#a51f
0xa537 23 inc hl
0xa538 10 dd djnz #a517
The c register, which contains bottom three bits of the byte we are currently handling, is subtracted
by one, and checked for zero. If we check the jump target address, it looks
like we end up at the place where we write the byte to our 0xC000 area. Of course, not to
0xC000 exactly, as that pointer is increased by 11 each time we run through
this little loop. If we do hit zero, hl is incremented, meaning we go from the seventh byte to the
eight byte in our compressed level data, and so on.
The conclusion we can draw here is that the bottom three bits represent the amount of times the top 5 bits need to be written out to our target decoding area of memory. All the rest is coordinate positioning and memory/register management. If you have some experience with programming, you might recognize this way of storing data. It is a simple run-length encoding!
Let's see how the memory area at 0xC000 gets filled up when we run this algorithm one write at a time.
Compared to the round:
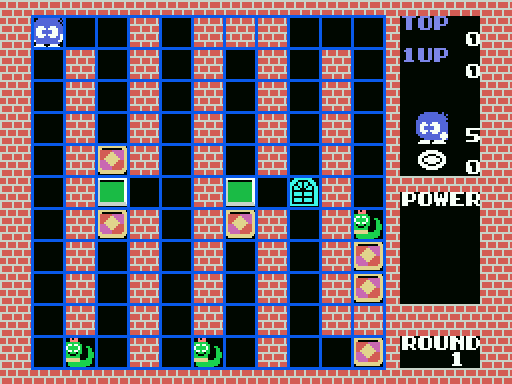
It seems this algorithm fills the board vertically first, then horizontally. That explains why we add 11 to the
0xC000 pointer every iteration, to reach the next position in the
same column. Let's see if our analysis is correct by decoding a couple bytes manually. It looks like Lolo, in the
top left corner has identifier 0x88, whereas walkable space is
0x08 and walls are 0x00.
The level data for round 1 looks like this, with the actual RLE-compressed data highlighted:
00 00 00 00 85 A5 88 0F 0A 07 00 20 0B A8 38 A8
0B 04 08 04 0F 0A 07 01 20 00 0B 38 A8 0B 04 08
04 0C F0 0D 07 00 0E 20 41 00 A8
Reminder: amount = bottom three bits plus 1, value = top five bits
-
Byte 1:
0x88 0b1000 1000: repeat value0x88(Lolo)1time -
Byte 2:
0x0F 0b0000 1111: repeat value0x08(Empty space)8times -
Byte 3:
0x0A 0b0000 1010: repeat value0x08(Empty space)3times -
Byte 4:
0x07 0b0000 0111: repeat value0x00(Wall)8times -
Byte 5:
0x00 0b0000 0000: repeat value0x00(Wall)1time -
Byte 6:
0x20 0b0010 0000: repeat value0x20(Snakey)1time - ...
Note that the maximum repetition amount we can encode this way is 8. We have three bits for the amount available, which gives us a range of zero to seven. One is added to this, to change the range to one to eight. It doesn't make sense to have zero as a repeat count, obviously. The stretch of walkable space in the first column, that spills over into the second column, has a repeat count of 11. Because of the three bit limitation, we do have to split this up into two instructions, the first for a repetition of eight, and then one for 3.
Unraveling algorithm #2
Remember how the sixth byte in our level data had the top bit determine whether a jump was taken or not? Let's see what happens if this top bit is not set for a level, and we do indeed take the jump. The check happened here:
0xa50c e6 80 and #80
0xa50e ca 5c a5 jp z,#a55c
Let's take another look at where we jump to:
0xa55c 7e ld a,(hl)
0xa55d e6 07 and #07
0xa55f 4f ld c,a
0xa560 0c inc c
0xa561 7e ld a,(hl)
0xa562 e6 f8 and #f8
0xa564 12 ld (de),a
0xa565 13 inc de
0xa566 0d dec c
0xa567 20 fb jr nz,#a564
0xa569 23 inc hl
0xa56a 10 f0 djnz #a55c
0xa56c 22 4d dd ld (#dd4d),hl
0xa56f 3e ff ld a,#ff
0xa571 12 ld (de),a
0xa572 c9 ret
This algorithm looks way simpler than the first one. We immediately notice the ANDing with
0x07 and 0xF8 again, after reading in the current byte of our
compressed level data. Exactly the same as the previous algorithm, so it looks like the encoding of repeat count and
value is identical.
Notice however what happens when we write the value to the de register, which contains
0xC000:
0xa564 12 ld (de),a
0xa565 13 inc de
We simply increase the de pointer! Instead of adding 11 to skip to the next position in the column, we
skip to the next one horizontally.
The conclusion we can draw is that algorithm 1 is a vertical encoding algorithm, and the second one is a horizontal
one. To make sure, let's look at how 0xC000 gets filled in when
we load a level that uses this second algorithm. An example of such a level would be round 5. This is the level data
for round 5:
00
00 00 21 81 24 0F 0C 88 0C F0 09 03 39 04 40 0F
09 40 08 28 0F 04 39 03 40 0F 09 40 08 28 0F 05
39 02 40 0F 09 40 08 28 0F
The sixth byte is 0x24, or 0b0010 0100. It does not have the top bit set.

When we take a look at 0xC000 when the decompression algorithm runs, we see the following:
This confirms that this second algorithm handles the decoding in a horizontal fashion.
Why two similar algorithms?
In modern day computing, memory space is not really an issue. Back in the early '80s though, you had to seriously
consider every option to cram as many bytes in your ROM cartridge as possible.
In this case, they only had 32 kilobytes to work with. When we take a look at the size of all the data of all the
levels in the ROM, conveniently stored sequentially, we see it ranges from
0x6D88 to 0x8B97. That's a total size of 7695 bytes, about a quarter of the entire
cartridge ROM!
If you simply look at certain levels, you immediately can tell whether they are better suited for a horizontal or a vertical algorithm. Round one and five are perfect examples of that.
We can't just guess the developer's intentions though, let's verify this! I've written some C++ code that can retrieve all the rounds from the ROM, and decode them. I've also implemented both horizontal and vertical encoding algorithms, so we can re-encode all the levels with both algorithms and see if they went for the smallest option each time.
Here's a list of all the rounds in the game, the length of the horizontal and vertical algorithms, which algorithm produces the smallest result, and the algorithm that was chosen by the developers.
| Round# | Horizontal size | Vertical size | Smallest algo | Chosen algo in ROM |
|---|---|---|---|---|
| Round 1 | 113 | 43 | Vertical | Vertical |
| Round 2 | 99 | 53 | Vertical | Vertical |
| Round 3 | 31 | 31 | Horizontal | Horizontal |
| Round 4 | 40 | 47 | Horizontal | Horizontal |
| Round 5 | 42 | 80 | Horizontal | Horizontal |
| Round 6 | 57 | 118 | Horizontal | Horizontal |
| Round 7 | 69 | 69 | Horizontal | Horizontal |
| Round 8 | 85 | 79 | Vertical | Vertical |
| Round 9 | 77 | 76 | Vertical | Vertical |
| Round 10 | 37 | 105 | Horizontal | Horizontal |
| Round 11 | 76 | 83 | Horizontal | Horizontal |
| Round 12 | 76 | 53 | Vertical | Vertical |
| Round 13 | 99 | 82 | Vertical | Vertical |
| Round 14 | 90 | 87 | Vertical | Vertical |
| Round 15 | 81 | 49 | Vertical | Vertical |
| Round 16 | 50 | 103 | Horizontal | Horizontal |
| Round 17 | 78 | 78 | Horizontal | Horizontal |
| Round 18 | 41 | 79 | Horizontal | Horizontal |
| Round 19 | 81 | 66 | Vertical | Vertical |
| Round 20 | 47 | 60 | Horizontal | Horizontal |
| Round 21 | 72 | 98 | Horizontal | Horizontal |
| Round 22 | 45 | 58 | Horizontal | Horizontal |
| Round 23 | 104 | 51 | Vertical | Vertical |
| Round 24 | 83 | 90 | Horizontal | Horizontal |
| Round 25 | 69 | 70 | Horizontal | Horizontal |
| Round 26 | 75 | 67 | Vertical | Vertical |
| Round 27 | 97 | 65 | Vertical | Vertical |
| Round 28 | 101 | 95 | Vertical | Vertical |
| Round 29 | 85 | 81 | Vertical | Vertical |
| Round 30 | 89 | 76 | Vertical | Vertical |
| Round 31 | 68 | 74 | Horizontal | Horizontal |
| Round 32 | 60 | 64 | Horizontal | Horizontal |
| Round 33 | 68 | 60 | Vertical | Vertical |
| Round 34 | 80 | 78 | Vertical | Vertical |
| Round 35 | 117 | 51 | Vertical | Vertical |
| Round 36 | 76 | 60 | Vertical | Vertical |
| Round 37 | 60 | 70 | Horizontal | Horizontal |
| Round 38 | 71 | 102 | Horizontal | Horizontal |
| Round 39 | 94 | 90 | Vertical | Vertical |
| Round 40 | 85 | 85 | Horizontal | Horizontal |
| Round 41 | 52 | 52 | Horizontal | Horizontal |
| Round 42 | 74 | 84 | Horizontal | Horizontal |
| Round 43 | 82 | 74 | Vertical | Vertical |
| Round 44 | 87 | 76 | Vertical | Vertical |
| Round 45 | 67 | 85 | Horizontal | Horizontal |
| Round 46 | 79 | 73 | Vertical | Vertical |
| Round 47 | 79 | 78 | Vertical | Vertical |
| Round 48 | 71 | 72 | Horizontal | Horizontal |
| Round 49 | 43 | 63 | Horizontal | Horizontal |
| Round 50 | 86 | 77 | Vertical | Vertical |
| Round 51 | 100 | 96 | Vertical | Vertical |
| Round 52 | 65 | 77 | Horizontal | Horizontal |
| Round 53 | 66 | 50 | Vertical | Vertical |
| Round 54 | 90 | 91 | Horizontal | Horizontal |
| Round 55 | 85 | 67 | Vertical | Vertical |
| Round 56 | 58 | 71 | Horizontal | Horizontal |
| Round 57 | 79 | 69 | Vertical | Vertical |
| Round 58 | 83 | 83 | Horizontal | Horizontal |
| Round 59 | 107 | 74 | Vertical | Vertical |
| Round 60 | 62 | 86 | Horizontal | Horizontal |
| Round 61 | 69 | 66 | Vertical | Vertical |
| Round 62 | 71 | 73 | Horizontal | Horizontal |
| Round 63 | 76 | 70 | Vertical | Vertical |
| Round 64 | 78 | 82 | Horizontal | Horizontal |
| Round 65 | 59 | 81 | Horizontal | Horizontal |
| Round 66 | 72 | 75 | Horizontal | Horizontal |
| Round 67 | 83 | 104 | Horizontal | Horizontal |
| Round 68 | 78 | 92 | Horizontal | Horizontal |
| Round 69 | 61 | 64 | Horizontal | Horizontal |
| Round 70 | 85 | 85 | Horizontal | Horizontal |
| Round 71 | 52 | 63 | Horizontal | Horizontal |
| Round 72 | 80 | 99 | Horizontal | Horizontal |
| Round 73 | 71 | 66 | Vertical | Vertical |
| Round 74 | 72 | 115 | Horizontal | Horizontal |
| Round 75 | 71 | 67 | Vertical | Vertical |
| Round 76 | 85 | 64 | Vertical | Vertical |
| Round 77 | 70 | 78 | Horizontal | Horizontal |
| Round 78 | 74 | 95 | Horizontal | Horizontal |
| Round 79 | 85 | 91 | Horizontal | Horizontal |
| Round 80 | 66 | 58 | Vertical | Vertical |
| Round 81 | 71 | 72 | Horizontal | Horizontal |
| Round 82 | 91 | 79 | Vertical | Vertical |
| Round 83 | 91 | 82 | Vertical | Vertical |
| Round 84 | 63 | 64 | Horizontal | Horizontal |
| Round 85 | 82 | 83 | Horizontal | Horizontal |
| Round 86 | 61 | 70 | Horizontal | Horizontal |
| Round 87 | 77 | 63 | Vertical | Vertical |
| Round 88 | 79 | 87 | Horizontal | Horizontal |
| Round 89 | 83 | 64 | Vertical | Vertical |
| Round 90 | 62 | 74 | Horizontal | Horizontal |
| Round 91 | 54 | 69 | Horizontal | Horizontal |
| Round 92 | 62 | 54 | Vertical | Vertical |
| Round 93 | 69 | 68 | Vertical | Vertical |
| Round 94 | 70 | 66 | Vertical | Vertical |
| Round 95 | 65 | 46 | Vertical | Vertical |
| Round 96 | 72 | 109 | Horizontal | Horizontal |
| Round 97 | 92 | 96 | Horizontal | Horizontal |
| Round 98 | 76 | 78 | Horizontal | Horizontal |
| Round 99 | 81 | 109 | Horizontal | Horizontal |
| Round 100 | 74 | 71 | Vertical | Vertical |
| Special round 101 | 79 | 79 | Horizontal | Horizontal |
| Special round 102 | 88 | 80 | Vertical | Vertical |
| Special round 103 | 63 | 83 | Horizontal | Horizontal |
| Special round 104 | 65 | 57 | Vertical | Vertical |
| Special round 105 | 99 | 100 | Horizontal | Horizontal |
| Bonus stage 1 | 55 | 101 | Horizontal | Horizontal |
| Bonus stage 2 | 44 | 42 | Vertical | Vertical |
| Bonus stage 3 | 78 | 80 | Horizontal | Horizontal |
| Bonus stage 4 | 64 | 91 | Horizontal | Horizontal |
| Bonus stage 5 | 93 | 54 | Vertical | Vertical |
| Bonus stage 6 | 66 | 71 | Horizontal | Horizontal |
| Bonus stage 7 | 68 | 69 | Horizontal | Horizontal |
| Bonus stage 8 | 45 | 54 | Horizontal | Horizontal |
| Bonus stage 9 | 54 | 95 | Horizontal | Horizontal |
| Bonus stage 10 | 63 | 52 | Vertical | Vertical |
| Bonus stage 11 | 55 | 101 | Horizontal | Horizontal |
| Bonus stage 12 | 44 | 42 | Vertical | Vertical |
| Bonus stage 13 | 78 | 80 | Horizontal | Horizontal |
| Bonus stage 14 | 64 | 91 | Horizontal | Horizontal |
| Bonus stage 15 | 93 | 54 | Vertical | Vertical |
| Bonus stage 16 | 66 | 71 | Horizontal | Horizontal |
| Bonus stage 17 | 68 | 69 | Horizontal | Horizontal |
| Bonus stage 18 | 45 | 54 | Horizontal | Horizontal |
| Bonus stage 19 | 54 | 95 | Horizontal | Horizontal |
| Bonus stage 20 | 63 | 52 | Vertical | Vertical |
This definitively proves that calculating both algorithm sizes and picking the smallest one is exactly what they did in the early '80s, when the puzzles were being created.
Some statistics:
- If only the horizontal algorithm was used, the total byte count would have been 9070 bytes.
- If only the vertical algorithm was used, the total byte count would have been 9333 bytes.
- If the optimal algorithm was used, the total byte count is/would have been 8273 bytes.
- If the worst algorithm was used, the total byte count is/would have been 10130 bytes.
Note that the discrepancy between 8273 bytes for the optimal algorithm and the previously mentioned 7695 bytes as is actually present in the ROM, is due to the fact that the last ten bonus levels are duplicated, but they are present only once in the ROM. It's just in our list of 25 pointers that the last two are identical to the previous two. In the statistics totals above, I counted the extra set of bonus stages as well. If I only count rounds 1 to 115, I end up exactly with 7695 bytes.
Back to the first five bytes
Now that we have figured out how to decode the run-length encoded data, we'll go back to the first five bytes. The first three were related to the powerups, and the next two were still unknown.
Both sets of data however, were copied to a different memory location by way of the ldir instruction.
0xa4b0 11 7b d8 ld de,#d87b
0xa4b3 01 03 00 ld bc,#0003
0xa4b6 ed b0 ldir
0xa4b8 11 8a d8 ld de,#d88a
0xa4bb 01 02 00 ld bc,#0002
0xa4be ed b0 ldir
Let's put a "read memory" watchpoint on the first target memory location (0xD87B) and see if we can
trigger it.
0x6732 21 7b d8 ld hl,#d87b
0x6735 11 35 d2 ld de,#d235
0x6738 01 03 00 ld bc,#0003
0x673b ed b0 ldir
For some reason, we are copying (with ldir) these same three bytes to yet another memory location,
0xD235. We'll put a "read memory" watchpoint on that location
instead. This watchpoint triggers during every frame of the game loop, and checks whether the correct amount of
diamond framers has been picked up, and the powerup needs to be activated or not.
0x56eb 21 35 d2 ld hl,#d235 ; 0xD235 = power up 1
0x56ee 06 00 ld b,#00
0x56f0 cd 00 57 call #5700
0x56f3 21 36 d2 ld hl,#d236 ; 0xD236 = power up 2
0x56f6 06 01 ld b,#01
0x56f8 cd 00 57 call #5700
0x56fb 21 37 d2 ld hl,#d237 ; 0xD237 = power up 3
0x56fe 06 02 ld b,#02
0x5700 7e ld a,(hl)
0x5701 4f ld c,a
0x5702 e6 c0 and #c0
0x5704 c8 ret z
0x5705 eb ex de,hl
0x5706 21 f4 d1 ld hl,#d1f4
0x5709 79 ld a,c
0x570a e6 3f and #3f
0x570c be cp (hl)
0x570d 20 2a jr nz,#5739
At the top of this code, we are loading the three different powerup values into the hl register, and we
call the function at 0x5700, just underneath.
Immediately, we see two AND operations being performed! First with 0xC0 and then with
0x3F. In binary, those look like this:
0xC0 = 1100 0000
0x3F = 0011 1111
Again, we are storing multiple pieces of information inside the powerup byte, this time in the top two bits, and the bottom six bits. We obviously know which types of information we need to store. It's the identifier of the powerup (be it nothing, arrow, emerald framer or bridge) and the amount of diamond framers we need to pick up to activate the powerup.
Logically, we can assume that the top two bits give us the identifier, and the bottom six the amount of diamond framers. Two bits gives us a possible 4 distinct values, and the bottom six gives us 64 possibilities. If we go in construction mode and we experiment with the diamond framer counter for the powerup, we see that it tops out at 63, for this exact reason.
Note that it is technically possible to have more than 63 diamond framers in a round, but because of the six bit limitation, the maximum we can reference is 63. I guess back in the '80s the decision was made that 63 as a maximum was a decent compromise.
Now, all that remains are the two mystery bytes in our level data, at position 4 and 5. When we put a watchpoint on the fourth byte, we end up here:
0x673d 3a 8a d8 ld a,(#d88a) ; 0xD88A = fourth byte
0x6740 cd 05 67 call #6705
0x6743 22 18 d0 ld (#d018),hl
0x6746 3e 05 ld a,#05
0x6748 32 1a d0 ld (#d01a),a
0x674b 3a 1c c8 ld a,(#c81c)
0x674e a7 and a
0x674f 20 0e jr nz,#675f
0x6751 3a 8b d8 ld a,(#d88b) ; 0xD88B = fifth byte
0x6754 cd 05 67 call #6705
0x6757 22 c7 d1 ld (#d1c7),hl
We notice the values being loaded, both the fourth and fifth byte, are immediately followed by a call to
0x6705. Now, this code isn't very clear, we're calling functions, setting
memory locations, and we don't have a clue what they do. In my reverse engineering before tackling decoding the
level data, I had already labeled several memory locations, which then popped up
here, giving me an immediate clue as to what was happening here. Let me repeat the same code, but with some extra
labels for these memory locations.
0x673d 3a 8a d8 ld a,(#d88a) ; 0xD88A = fourth byte
0x6740 cd 05 67 call #6705
0x6743 22 18 d0 ld ($lolo_pos_y),hl
0x6746 3e 05 ld a,#05
0x6748 32 1a d0 ld ($lolo_direction_facing),a
0x674b 3a 1c c8 ld a,($current_bonus_round)
0x674e a7 and a
0x674f 20 0e jr nz,#675f
0x6751 3a 8b d8 ld a,(#d88b) ; 0xD88B = fifth byte
0x6754 cd 05 67 call #6705
0x6757 22 c7 d1 ld ($exit_door_y),hl
This gives away the secret immediately, the fourth and fifth byte in our level data stores the position of Lolo and
the exit. But, there is a conversion going on! We see the result of the
call to 0x6705, the hl register contents being written to $lolo_pos_y, but remember that
the hl register is 16-bit. In the game, Lolo's position is
stored as one byte for the y-coordinate, and one byte for the x-coordinate. So ld ($lolo_pos_y),hl
actually loads both y and x into the correct memory location.
The function at 0x6705 must therefore convert our single byte from the level data into a y,x
coordinate. Let's take a look at this function:
0x6705 67 ld h,a
0x6706 e6 0f and #0f
0x6708 87 add a,a
0x6709 87 add a,a
0x670a c6 02 add a,#02
0x670c 6f ld l,a
0x670d 7c ld a,h
0x670e e6 f0 and #f0
0x6710 0f rrca
0x6711 0f rrca
0x6712 c6 04 add a,#04
0x6714 67 ld h,a
0x6715 c9 ret
We can divide this function in two sections. Notice that on the first line we are saving our incoming value (the
a register) to register h. We then do a few
manipulations on that same a register, only to load our stored value from h back in to
a on line 0x670D. Then, we do some more
manipulations.
The first half of this function operates on the bottom four bits of our input data, because we AND with
0x0F, or 0000 1111. Looking ahead to the second
part of the function, we do the same ANDing, but with the top nibble, so 0xF0, or
1111 0000.
The first part continues: we add a to itself (in other words we double the value) twice, and add 2.
The second part, instead of doubling twice, halves the value twice (through the rrca instruction,
rotate right with carry), and adds four.
Let's see if our interpretation is correct by looking at round 1.
For Lolo's y coordinate, we take the bottom nibble of 0x00, which is 0x00, double it
twice and add 2:
0 * 2 * 2 + 2 = 2
For Lolo's x coordinate, we remove the bottom nibble of 0x00, which is 0x00, halve it
twice and add 4:
0 / 2 / 2 + 4 = 4
For the exit's y coordinate, we take the bottom nibble of 0x85, which is 0x05, double it
twice and add 2:
5 * 2 * 2 + 2 = 22
For the exit's x coordinate, we remove the bottom nibble of 0x85, which is 0x80, halve it
twice and add 4:
128 / 2 / 2 + 4 = 36

At first sight, these values don't seem to make a whole lot of sense when we look at the grid above. However, we have to take into account the fact that Lolo can stand halfway past a block, and not only that, every time you move, Lolo takes a half-step in-between that as well. Even though we have an 11 by 11 grid, the tiles can be positioned 4 times as precise.
We would expected to have Lolo positioned at 0, 0 in the first round, as he is in the top left corner, yet our coordinates come out at x:4 y:2. This makes perfect sense if we take the stone tiled wall around the level into account. Our origin point therefore doesn't lie in the top-left of our 11 by 11 grid, but at the top-left of the entire screen.

In the grid above, with the origin (0, 0) at top left, Lolo is indeed positioned at x:4, y:2.
While it's interesting to know how the internal coordinate system works, it doesn't help us much with interpreting
how the two level data bytes representing these positions are encoded.
Looking again at these two values, Lolo at 0x00 and the exit at 0x85, the solution is
staring us in the face if we look at Lolo and the exit's position in our 11 by
11 grid. Lolo is positioned at 0, 0 and the exit is at 8, 5. Compare that with 0x00 and
0x85, surely that can't be a coincidence. It's a simple representation of the x and y values! X in the
top nibble, y in the bottom nibble.
We can easily confirm this by looking at these positions in other rounds, and yes this is indeed the case. Now we have figured out how an entire round is encoded.
A mystery within Eggerland Mystery?
There is something peculiar going on with the file header of .pzl files. If we save the first five
rounds untouched, the file looks like this, with the file header highlighted:
FE F8 D5 C9 D6 00 00 00 00 00 00 85 A5 88 0F 0A
07 00 20 0B A8 38 A8 0B 04 08 04 0F 0A 07 01 20
00 0B 38 A8 0B 04 08 04 0C F0 0D 07 00 0E 20 41
00 A8 00 00 00 82 88 AF 0F 0B 07 09 40 0E 38 40
38 08 07 0A 00 0A 18 40 0C 04 38 02 08 40 0B 18
0B 40 01 38 01 08 03 08 00 08 88 09 38 09 F0 00
09 38 02 08 02 0F 0C 00 00 00 11 99 19 0F 0B 88
0F 0F 0E 48 0A 58 0F 0F 0A 40 0F 0F 0A 50 0A 30
0F 0F 0E F8 0F 0B 00 00 00 52 59 22 0F 0F 0F 08
40 08 88 08 40 0F 0E 38 0E 38 0A 38 0C 38 0C 10
08 40 08 10 0B 03 38 03 0F 0F 08 F0 0F 0F 00 00
00 21 81 24 0F 0C 88 0C F0 09 03 39 04 40 0F 09
40 08 28 0F 04 39 03 40 0F 09 40 08 28 0F 05 39
02 40 0F 09 40 08 28 0F
This file header is not part of the level data, but if we look closer, we see some numbers we recognize! Let's rearrange the bytes a bit:
FE
F8 D5
C9 D6
00 00
If we account for endianness, there seem to be two pointers in there, 0xD5F8 and 0xD6C9.
The first pointer, 0xD5F8 is the first pointer in our big list
of 25, it represents the start of the first five rounds. These rounds take up 209 bytes, and if we add this to
0xD5F8, we get the second pointer in our file header,
0xD6C9! It looks like these pointers specify the range of data we need to overwrite in RAM, when we
load our custom rounds.
Specifying start and end pointers of this new data leads me to believe that they might have intended to replace other sets of five rounds, not just the first set of five. These pointers would indicate where to write this data. Of course, the decision was made to only load the first five into RAM (which is overwritable), so it's not really possible to overwrite e.g. rounds 6-10.
Let's look at the code where the file header is being handled:
0xa651 cd 6b a7 call #a76b
0xa654 20 41 jr nz,#a697
0xa656 ed 5b 2e d9 ld de,(#d92e)
0xa65a cd b6 a6 call #a6b6 ; load header byte 1 into a
0xa65d fe fe cp #fe
0xa65f 20 36 jr nz,#a697
0xa661 cd b6 a6 call #a6b6 ; load header byte 2 into a
0xa664 cd b6 a6 call #a6b6 ; load header byte 3 into a
0xa667 cd b6 a6 call #a6b6 ; load header byte 4 into a
0xa66a cd b6 a6 call #a6b6 ; load header byte 5 into a
0xa66d cd b6 a6 call #a6b6 ; load header byte 6 into a
0xa670 6f ld l,a
0xa671 cd b6 a6 call #a6b6 ; load header byte 7 into a
0xa674 67 ld h,a
0xa675 22 bf fc ld (#fcbf),hl
0xa678 b5 or l
0xa679 20 03 jr nz,#a67e
0xa67b 11 f8 d5 ld de,#d5f8
0xa67e cd b6 a6 call #a6b6
0xa681 20 0c jr nz,#a68f
0xa683 12 ld (de),a
0xa684 13 inc de
0xa685 21 00 e0 ld hl,#e000
0xa688 a7 and a
0xa689 ed 52 sbc hl,de
0xa68b 28 c2 jr z,#a64f
0xa68d 18 ef jr #a67e
0xa68f cd 7e a7 call #a77e
0xa692 c2 11 a6 jp nz,#a611
0xa695 a7 and a
0xa696 c9 ret
After the first byte on disk is loaded into register a (done with the call to 0xA6B6), on
line 0xA65A, there's a comparison with the hard-coded value
0xFE. This looks to be a magic number to identify Eggerland Mystery puzzle files.
Then, we see 4 bytes being read, and basically thrown away. Our two pointers reside in bytes 2, 3, 4, and 5, yet here they are completely unused. Another hint that they intended to make it possible to load custom levels above the first five rounds, but ultimately scrapped the idea, and just ignored these bytes.
Byte 6 and 7, which always seem to be 0x0000 in the file, look like they are special. The two combined
bytes are written to location 0xFCBF, and then the two bytes are
OR-ed together. If the result of that OR is not zero, a small jump is taken, skipping the
ld de,#d5f8 line. This load instruction loads the target
address of the first round into the de register, where subsequently all the bytes of the puzzle file
will be copied into.
Basically, these two bytes, if non-zero prevent the write target pointer being set to our well known value. Another hint that the writing of round data was dynamic enough to target other pointers.
When I look at the file-writing routine though, the sixth and seventh byte always seem to be written as
0x0000.
The file loading code when reading from tape is slightly different when it comes to what is skipped when the
OR of bytes 6 and 7 results in a non-zero flag, but it ultimately
leads to the same result.
I wonder what the reason was to decide to only allow the first rounds to be overwritten. Was it lack of available memory? Or was it the complexity of managing overwriting variable sized chunks of data? If the puzzle file contains a chunk of data that is bigger than the original 5 rounds in memory, you'd have to shuffle some memory around to allow them to fit.
The answer to this question cannot be easily deduced from the code we have in front of us, unfortunately.
What can we do with this information?
Now that I'm able to encode and decode level data, I'm also able to recreate the construction mode. This is exactly what I have done, and it is available online here, reimplemented in javascript.
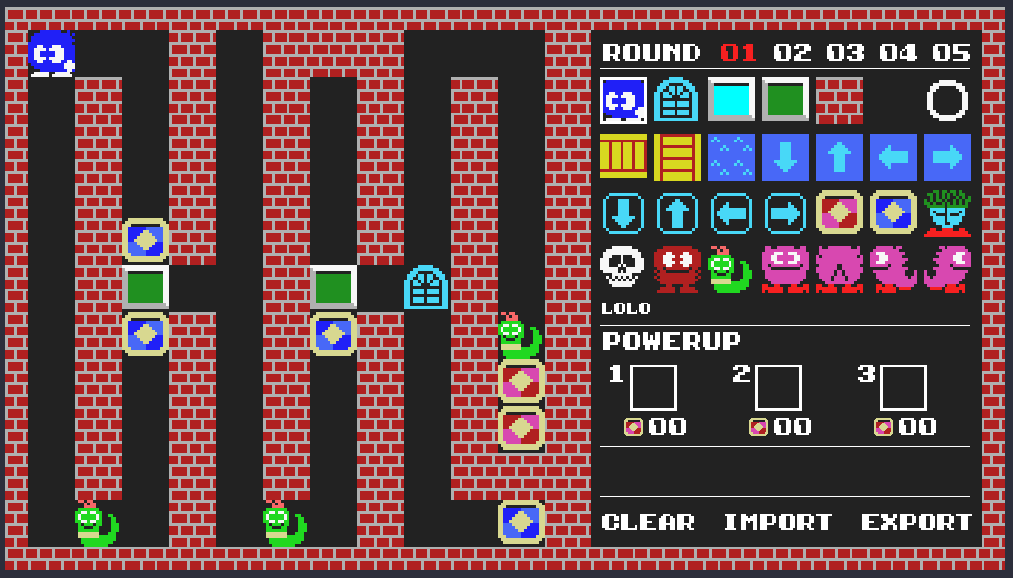
You can load all 125 rounds from the original game, or load custom puzzle files, and export them as well so you can play them in the game.
I have also dumped all the rounds. How all the rounds looked has been available for a long time of course, I remember seeing them in magazines in the mid '80s. However, what knowing the decoding algorithm allows us to do is to export the hidden information as well, such as respawn locations, water flow directions and powerup diamond framer counts.
The list of levels is available here.

If you want to watch me do this type of reverse engineering live, follow me on twitch.tv/zappatic, or check out my YouTube channel.